

Una distribuzione di cariche elttriche, ferme rispetto all'osservatore, genera in un dato punto dello spazio un campo elettrico con modulo, direzione e verso che non variano nel tempo, cioè un campo elettrico stazionario.
Facciamo in modo che il campo elettrico non sia più stazionario ma risulti variabile nel tempo. Consideriamo una situazione semplice: un condensatore piano ha le armature collegate ai morsetti di un generatore di forma elettromotrice fem attraverso una resistenza R ed un interruttore I.
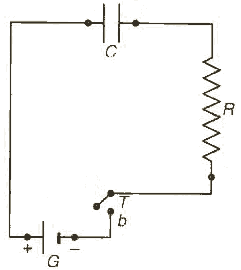
Appena l'inerruttore si chiude, nasce una corrente di conduzione dal positivo al negativo (per convenzione). Questa corrente è costituita d aun flusso di elettroni che si muovono in senso contrario e produce un accumulo di carica positiva e di carica negative sulle rispettive armature del condensatore.
Contemporaneamente fra le armature nasce una differenza di potenziale ddp che aumenta con il tempo, tendendo a raggiungere il valore fem con la legge espressa dalla relazione:
Per conseguenza fra le armature, distanti d l'una dall'altra, si stabilisce un campo elettrico praticamente uniforme il cui modulo, dato da E=ddp/d, varia anch'esso con il tempo, proprio come varia ddp.Inoltre anche la carica q=C*ddp sulle armature varia con il tempo come ddp.
Ora se delta t è un intervallo di tempo sufficientemente piccolo, il rapporto delta q/delta t indica la rapidità con la quale si accumula la carica sulle armature e misura evidentemente l'intensità di corrente che scorre nel circuito:

A questo punto cxonsideriamo una superficie chiusa che avvolge l'armatura con le cariche positive ed osserviamo che in ogni istante il flusso del campo elettrico uscente da questa superficie, per la legge di Gauss, è uguale alla carica q accumulata sull'armatura divisa per la costante epsilon0:
Siccome la carica q varia nel tempo, dovrà variare anche il flusso di E. Così, in un dato intervallo di tempo delta t, alla rapidità delta q/deltat con la quale cresce la carica positiva sull'armatura in questione corrisponderà la rapidità deltafis(E)/delta t con la quale aumenta il flusso del campo elettrico che esce dalla superficie:
Come delta q/delta t indica la corrente di conduzione che, scorrendo nel circuito, entra nella superficie che avvolge l'armatura in questione, così anche alla quantità epsilon0*fis(E)/delta t si attribuisce il significato di una corrente che esce da quella superficie. E' la cosiddetta corrente di spostamento:
Il concetto di corrente di spostamento così introdotto può essere esteso a situazioni ben più generali. cioè: se una regione è sede di un campo elettrico variabile nel tempo, il prodotto della costante dielettrica (epsilon0 se la regione è vuota, epsilon se è riempita di materia) per la rapidità di variazionedel flusso di questo campo attraverso una generica superficie disposta in quella regione misura l'intensità della corrente di spostamento relativa alla superficie.
Per chiarire ulteriormente il concetto fondamentale di corrente di spostamento, vale sottolineare la differenza fisica che esiste fra corrente di conduzione e la corrente di spostamento:
Sappiamo che la corrente di conduzione, come quella che scorre in un filo metallico, genera nello spazio circostante un campo magnetico. Così intorno al filo che conduce la corrente all'armatura con le cariche positive, durante il processo di carica, si produce un campo magnetico secondo la legge di Biot-Savart. La domanda che ora viene spontanea è se la corrente di spostamento, come quella di conduzione, generi un campo magnetico.
Se la risposta a questa domanda fose affermativa, intorno alla regione compresa fra le armature, dove cessa ogni corrente di conduzione ed è presente la corrente di spostamento is=epsilon0*deltafis(E)/delta t, si dovrebbe poter riscontrare sperimentalmente l'esistenza di un campo magnetico.
Ebbene, ogni volta in una data regione si produce un campo elettrico variabile, si genera anche un campo magnetico. Si dice così che si ha un campo magnetico indotto.Per questo campo valgono le medesime proprietà viste per quello prodotto da una corrente di conduzione.
per vedere la relazione che passa fra campo elettrico variabile nel tempo e campo magnetico indotto, premetto questo: si consideri una linea l piana chiusa arbitrariamente orientata e la superficie S anch'essa piana che ha per contorno la linea scelta e su questa superficie fissiamo la normale n arbitrariamente orientata. Dirò allora che la linea è orientata in senso positivo quando un osservatore ideale disposto come la normale vede la lineas percorsa nel senso antiorario.
Ciò premesso, si supponga che la linea chiusa si trovi in una regione sede di un campo elettrico variabile. In questa situazione si chiama corrente di spostamento concatenata con la linea il prodotto della costante dielettrica epsilon0 per la rapidità con cui varia il flusso del campo elettrico attraverso la superficie S che ha per contorno la linea stessa:
Ciò che l'esperienza mette in evidenza è che:
Si immagini un campo elettrico uniforome e variabile nel tempo in una regione cilindrica di spazio. Le linee del campo magneticxo prodotto da questo campo elettrico variabile sono, per motivi di simmetria, circonferenze con i vari centri sull'asse della regione cilindrica e ortogonali al campo elettrico stesso.
Per tener conto del fatto fondamentale che a produrre un campo magnetico contribuiscono sia le correnti di conduzione che quelle di spostamento la legge di Ampère deve essere modificata in modo da conglobare al legge di Maxwell:
 . Questa è una relazione fondamentale dell'elettromagnetismo nota con il nome di Ampère-Maxwell.
. Questa è una relazione fondamentale dell'elettromagnetismo nota con il nome di Ampère-Maxwell.
Fu J.C. Maxwell a proporre la modifica della legge di Ampère per esigenze puramente logiche. E' possibile infatti dimostrare che la legge di Ampère è in contraddizione con la legge della conservazione della carica elettrica. Questa contraddizione viene eliminata, appunto, considerando, accanto alla corrente di conduzione, anche quella di spostamento. L'importanza di questa aggiunta è stata incalcolabile ai fini dello sviluppo scientifico e tecnologivo.