| Indice | indietro | avanti |
Moto circolare uniforme

L'aggettivo uniforme non deve ingannare: il moto è comunque accelerato perchè la velocità varia in direzione. L'aggettivo uniforme si riferisce al fatto che il modulo della velocità rimane costante.
In un moto circolare uniforme la forza (e quindi anche l'accelerazione) sono sempre radiali, cioè costantemente perpendicolari alla velocità. Dato che la velocità è tangente alla traiettoria, la forza e l'accelerazione sono sempre dirette verso il centro della circonferenza (forza centripeta e accelerazione centripeta).
Attenzione! Non è il moto circolare uniforme a creare la forza centripeta, ma è la forza centripeta che causa questo tipo di moto.
Analizziamo tre esempi diversii:
- Il moto della Luna intorno alla Terra: La traiettoria della Luna è praticamente circolare, la forza centripeta è fornita dall'attrazione gravitazionale esercitata su di essa dalla Terra. Questa attrazione costringe la Luna a curvare continuamente e a rimanere legata alla Terra, senza di essa, la Luna proseguirebbe di moto rettilineo uniforme.
- Un'automobile che curva: la forza centripeta necessaria per curvare è fornita dalla forza di attrito statico di aderenza tra gomme e strada (statico e non dinamico perché non c'è moto nella direzione radiale, ma solo in quella tangenziale); se la massima forza di attrito statico non è sufficiente, come nel caso di strada ghiacciata, l'auto non riesce a tenere la curva.
- Un sasso che ruota legato ad una corda: è la tensione della corda che gioca il ruolo di forza centripeta: se la corda si rompe, il sasso partirà per la tangente secondo la direzione della velocità in quell'istante. E' quello che succede, per esempio, nel lancio del martello, dove, per la verità, la velocità viene via via aumentata fino al lancio (e questo significa che la forza ha una componente radiale ed una tangenziale).

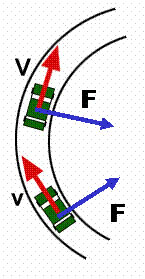
La forza necessaria per curvare dipende dalla velocità dell'auto
La forza necessaria per curvare dipende dalla massa dell'auto
La forza necessaria per curvare dipende dal raggio di curvatura
E' esperienza comune che sia più difficile tenere la curva a forte velocità: la forza necessaria a tenere la curva dipende fortemente dalla velocità; se un'automobile affronta una curva a velocità sostenuta, il rischio di uscire di strada è molto alto.
La massa inerziale influisce (l'inerzia è la tendenza a mantenere il proprio stato di moto): ci vuole più forza per far curvare un autotreno, rispetto a quella che ci vuole per far curvare una moto.
Un raggio di curvatura minore corrisponde ad una curva più stretta: all'aumentare del raggio la forza necessaria diminuisce.
F = m v2 / R
Individuiamo alcune grandezze che caratterizzano il moto circolare uniforme:
Il periodo T del moto è l'intervallo di tempo (sempre uguale) in cui il corpo compie un giro completo. Il moto circolare uniforme è periodico perchè si ripete sempre uguale per ogni intervallo di tempo T.
In tutti i moti periodici si definisce la frequenza f del moto come l'inverso del periodo. Essa rappresenta il numero di giri compiuti nell'unità di tempo e si misura in hertz (simbolo Hz).
1 Hz = 1 s-1
Il vettore velocità v ha direzione istante per istante tangente (si chiama anche velocità tangenziale) alla traiettoria circolare. Il modulo della velocità invece rimane costante ed è dato dal rapporto tra la lunghezza della circonferenza e il periodo.
Attenzione! Per determinare il modulo della velocità tangenziale si considera la lunghezza scalare della traiettoria e non il vettore spostamento s che, alla fine di un giro, è nullo.
| Dati del problema | Richieste | ||
| T = 28 giorni = 2,42 106 s | periodo di rivoluzione della Luna | v | velocità della Luna |
| R = 3,82 108 m | distanza Terra-Luna | f | frequenza della Luna |
La velocità di rivoluzione della Luna intorno alla Terra vale v = 2 π 3,82 108 m / 2,42 106 s = 991 m/s
La frequenza del moto è f = 1 /2,42 106 s = 4,13 10-7 Hz
| Indice | indietro | avanti |
Copyleft Ludovica Battista