| Indice | indietro | avanti |
Principio fondamentale della dinamica
Se le forze agenti su un corpo non sono equilibrate, il corpo cambia la sua velocità cioè accelera. Ricorda che un'accelerazione non è necessariamente un aumento di velocità, ma un suo generico cambiamento. Poichè la velocità è un vettore, la variazione può coinvolgerne l'intensità o anche la direzione e il verso.
Analizziamo i dati ottenuti dal moto di una slitta a cuscino d'aria di 400 g che viene tirata da una forza rappresentata da un pesetto libero di cadere e legato alla slitta da un filo sottile che passa attraverso una carrucola. L'unica forza non equilibrata sulla slitta è la forza trainante orizzontale poichè la forza peso è compensata dal vincolo della rotaia e la forza d'attrito è praticamente nulla a causa del cuscino d'aria che si forma sotto la slitta. All'inizio la slitta è inizialmente trattenuta da un'elettrocalamita e, nell'istante in cui essa viene disinserita, parte anche un cronometro digitale che si ferma quando essa passa attraverso una fotocellula opportunamente distanziata. Variando la posizione della fotocellula si ottiene una tabella di tempi t e spostamenti s corrispondenti. Il grafico orario che ne risulta è parabolico, segno che il moto è uniformemente accelerato. L'accelerazione si può ricavare dall'analisi dei grafici orari oppure utilizzando la legge oraria del moto uniformemente accelerato (con velocità iniziale nulla):
a = 2 s / t2
Al variare della forza trainante (ottenuta con pesi di massa diversa) si costruisce una tabella che mette in relazione l'accelerazione a ed il valore della forza trainante F insieme all'incertezza relativa sulla misura dell'accelerazione. (I dati sono tratti da un'esperienza effettivamente svolta in un laboratorio scolastico). Nel grafico relativo, come si vede, si può facilmente tracciare una retta tra i punti sperimentali.
| F(mN) | a(cm/s2) | incertezza |
| 98 | 27,1 | 1,3% |
| 147 | 38,9 | 0,7% |
| 196 | 49,7 | 0,6% |
| 245 | 59,4 | 1,0% |
| 294 | 71,4 | 1,3% |
La retta non passa per l'origine, come ci si sarebbe aspettato, a causa del non perfetto livellamento del piano della rotaia che causa un errore sistematico sulle misure. E' come se fosse sempre presente una piccola componente della forza di gravità.
Dai dati e soprattutto dal grafico possiamo vedere che tra l'accelerazione della slitta e la forza risultante c'è una correlazione lineare. La pendenza della retta è anche una misura del coefficiente di proporzionalità tra le due grandezze. Esso vale k = 4 mN s2/cm = 0,4 N s2/m. Quale sarà il suo significato fisico?
la stessa accelerazione di prima
un'accelerazione metà
un'accelerazione doppia
Puoi avere un'idea della correttezza delle tue ipotesi, osservando questa seconda serie di dati sperimentali in cui sono riportate, a parità di forza trainante, le accelerazioni subite da slitte di massa diversa.
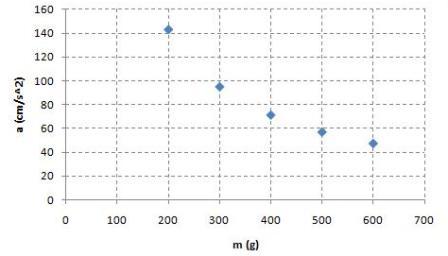
| m(g) | a(cm/s2) |
| 200 | 142,9 |
| 300 | 95,1 |
| 400 | 71,4 |
| 500 | 57,2 |
| 600 | 47,6 |
Come si vede, l'accelerazione diminuisce all'aumentare della massa e, poichè i punti sperimentali del grafico corrispondente sono correlati in modo iperbolico, questa volta possiamo parlare di relazione di proporzionalità inversa. Ricordiamo che due grandezze sono inversamente proporzionali quando il loro prodotto è costante!
Riassumendo, possiamo concludere che:
- a parità di massa, l'accelerazione è direttamente proporzionale alla forza risultante;
- a parità di forza, l'accelerazione è inversamente proporzionale alla massa.
Come mettere insieme queste due relazioni in una sola legge? Il secondo principio (o principio fondamentale) della dinamica di Newton può enunciarsi nel modo seguente:
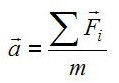(equazione vettoriale)dove
rappresenta la risultante vettoriale di tutte le forze agenti sul corpo.Le dimensioni fisiche della forza devono essere pertanto quelle di una massa per una accelerazione ([forza] = [massa] * [accelerazione]) e la definizione del newton (simbolo N) nel Sistema Internazionale dipende dalle unità SI di massa e di accelerazione:
1 N = 1 kg m / s2
Nei Principii di filosofia naturale di Newton si legge:
| Axiomata sive Leges Motus Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur. | Seconda legge della dinamica: L'accelerazione (mutamento del moto) è proporzionale alla risultante delle forze esterne (forza motrice impressa) ed ha la stessa direzione e verso (segue la retta) della forza. |
L'equazione vettoriale che esprime il secondo principio equivale a 3 equazioni scalari: per ognuno
dei tre assi spaziali si ha che la componente dell'accelerazione si ottiene dividendo la componente
corrispondente della forza per la massa (che è uno scalare):
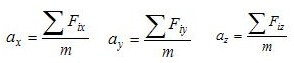
| Indice | indietro | avanti |
Copyleft Ludovica Battista