| Indice | indietro | avanti |
I radianti e la velocità angolare
I gradi di libertà del moto di un corpo sono determinati dal numero di coordinate necessarie per individuare la posizione del corpo nello spazio.
Quanti gradi di libertà ha un punto P che si muove di moto circolare uniforme? Si ha bisogno di grandezze vettoriali per descrivere questo tipo di moto?
Se un corpo puntiforme può muoversi liberamente nel piano, allora la posizione, lo spostamento, la velocità e l'accelerazione sono individuate da due coordinate (due gradi di libertà) ed è necessario ricorrere a grandezze vettoriali. E' il caso di osservare che, dopo un percorso chiuso, il vettore spostamento e il vettore velocità media risultano nulli.
Se invece consideriamo il punto vincolato sulla circonferenza come un treno
sui binari possiamo disinteressarci al fatto che la traiettoria sia curva e
descriverne il moto con una sola coordinata che ne indichi
la posizione sul binario o sulla circonferenza.
Analogamente la velocità si calcola in base alla lunghezza scalare dello spazio percorso.
Un corpo vincolato a muoversi lungo una linea curva ha un solo grado di libertà.
Il punto P che si muove di moto circolare uniforme percorre, in un periodo T,
un tratto 2 π R pari alla lunghezza della circonferenza con velocità tangenziale
v = 2 π R / T.
La velocità tangenziale di P è quella che il punto avrebbe se percorresse un tratto
2 π R di moto rettilineo.

La posizione del punto P rispetto ad un riferimento Oxy con origine coincidente con il centro della circonferenza può essere individuata sia da coordinate cartesiane (x, y), sia da coordinate polari (R, α) dove R è il raggio (fisso) della circonferenza e α è l'angolo formato dal raggio con l'asse x.
Poichè le componenti cartesiane della posizione, della velocità e dell'accelerazione cambiano continuamente nel tempo, è più conveniente utilizzare un riferimento polare: il raggio R rimane costante e il moto è descritto al variare nel tempo della sola coordinata α.
La misura in radianti dell'angolo α si ottiene facendo il rapporto α = arco di circonferenza /raggio.
| angolo (in gradi) | angolo (in rad) (i valori sono approssimati in quanto numeri irrazionali. E' sempre meglio esprimere il valore dell'angolo in radianti in funzione di π) |
| 0° | 0,00 |
| 30° | 0,52 (π/6) |
| 45° | 0,79 (π/4) |
| 60° | 1,05 (π/3) |
| 90° | 1,57 (π/2) |
| 120° | 2,09 (2π/3) |
| 180° | 3,14 (π) |
| 360° | 2,28 (2π) |
Per passare da gradi sessagesimali a radianti (e viceversa), si tiene conto della seguente proporzione:
La velocità con cui l'angolo α varia nel tempo si chiama velocità angolare. Questa grandezza non è omogenea alla velocità tangenziale, le sue dimensioni fisiche sono infatti:
l'unità di misura è il radiante al secondo (rad/s)
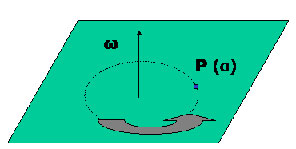
La velocità angolare ω è un vettore che ha direzione
perpendicolare al piano della traiettoria circolare e verso rivolto dalla
parte in cui la rotazione si vede in senso antiorario.
Il modulo si ottiene facendo il rapporto tra l'angolo giro (2π) ed il periodo T:
v = ω R
F = m ω2 R
F = m ω2 / R
f = ω / 2 π
ω = 2 π T
| Indice | indietro | avanti |
Copyleft Ludovica Battista