| Indice | indietro | avanti |
Confronto di grafici
Nella legge oraria del moto armonico la posizione x è espressa in funzione del tempo t:
compare la costante φ0 detta fase iniziale. Questa costante (espressa in radianti) dipende dalla posizione iniziale del corpo che si calcola ponendo t=0.
La tabella seguente fornisce qualche esempio:
| caso | Posizione iniziale | Valore del coseno | Fase iniziale | Legge oraria |
| 1 | A | cos (φ0) = 1 | φ0 = 0 | x (t) = A cos (ω t) |
| 2 | -A | cos (φ0) = -1 | φ0 = π | x (t) = A cos (ω t + π) |
| 3 | A/2 | cos (φ0) = 1/2 | φ0 = π/3 | x (t) = A cos (ω t + π/3) |
| 4 | 0 | cos (φ0) = 0 | φ0 = π/2 | x (t) = A cos (ω t + π/2) |
Scrivere la legge del moto significa determinare il valore delle costanti A (ampiezza), ω (pulsazione) e φ0 (fase iniziale).
| Dati del problema | Richieste | ||
| m = 2 kg | massa dell'oggetto | A | ampiezza |
| k = 100 N/m | costante elastica | ω | pulsazione |
| x(0) = 1 m | posizione iniziale | φ0 | fase iniziale |
| v(0) = 0 | velocità iniziale | x (t) = A cos (ω t + φ0) | legge oraria del moto |
Al tempo 0 il corpo ha velocità 0, quindi la posizione iniziale corrisponde allo spostamento massimo A dalla posizione di equilibrio: x (0) = A = 1 m
Per quanto visto prima, a questa posizione iniziale corrisponde la fase iniziale: φ0 = 0
Infine la pulsazione ω si determina con la relazione:
![]() = 7 rad/s
= 7 rad/s
La legge oraria del moto è pertanto: x (t) = cos (7 t)
- stessa frequenza e stessa ampiezza
- stessa ampiezza e frequenza differente
- stessa frequenza ed ampiezza differente

- stessa frequenza e stessa ampiezza
- stessa ampiezza e frequenza differente
- stessa frequenza ed ampiezza differente

- stessa ampiezza e diversa frequenza
- stessa frequenza, stessa ampiezza e stessa fase iniziale
- stessa frequenza, stessa ampiezza e diversa fase iniziale
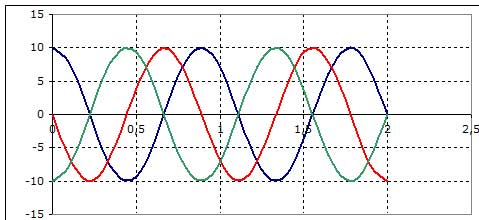
La differenza di fase tra una sinusoide ed un'altra che hanno la stessa frequenza si dice sfasamento. La curva blu e la curva rossa nell'ultimo grafico hanno uno sfasamento di π/2 (cioè 1/4 di periodo), mentre la curva blu e la curva verde hanno uno sfasamento di π (cioè mezzo periodo). Due sinusoidi sfasate di π si dicono in opposizione di fase. Due sinusoidi con sfasamento nullo si dicono in fase