| Indice | indietro | avanti |
Stati legati
 |
Rifiuti in orbita (immagine diffusa dall'Ente spaziale Europeo) Ci sono circa 12 000 oggetti in orbita intorno alla Terra, di cui soltanto 800 sono satelliti in attività. Il resto è spazzatura, cioè vecchi satelliti e frammenti. Perchè alcuni corpi rimangono intrappolati nel campo gravitazionale terrestre e altri riescono a sfuggire? |
| Dati del problema | Richieste | |
| M = 6 1024 kg | massa della Terra | orbita aperta o chiusa? |
| m | massa del meteorite | |
| d = 3 107 m | distanza iniziale del meteorite dalla Terra | |
| v = 8 km/s = 8 000 m/s | modulo della velocità iniziale del meteorite (rispetto alla Terra) |
Affronteremo il problema con considerazioni energetiche: Come è stato già detto, conviene mettersi nel sistema di riferimento di una delle due masse in modo da averne una immobile e l'altra a velocità v rispetto all'altra. In questo caso il riferimento più conveniente è quello solidale alla Terra. In questo riferimento l'energia meccanica E del sistema Terra + meteorite è:
E = K + U = 1/2 m v2 - G M m / d = costante
L'energia meccanica totale rimane costante, mentre la velocità v del meteorite e la sua distanza d dal centro della Terra variano istante per istante. Il comportamento successivo del meteorite dipende dal valore di E e più precisamente dal suo segno. Vediamo perché.

Supponiamo che l'energia meccanica E sia positiva. In questo caso si ha che K > |U|
Nella curva dell'energia in funzione della distanza d dalla Terra, l'energia potenziale U è in blu e l'energia meccanica totale E è in rosso.
Per sfuggire all'attrazione gravitazionale, il meteorite deve allontanarsi dalla Terra. All'aumentare della distanza l'energia potenziale U cresce tendendo a zero e l'energia cinetica K (data dalla differenza E - U) diminuisce. A distanza infinita l'energia potenziale è nulla, ma tuttavia, poichè l'energia totale è positiva, rimane sempre dell'energia cinetica che permette al meteorite di allontanarsi di più e definitivamente dalla Terra.
In pratica a distanze molto grandi, se l'energia meccanica totale è positiva, il meteorite può considerarsi libero dall'attrazione terrestre.
Il meteorite percorrerà un'orbita aperta (un ramo di iperbole) che non lo riporterà più nelle vicinanze della Terra.
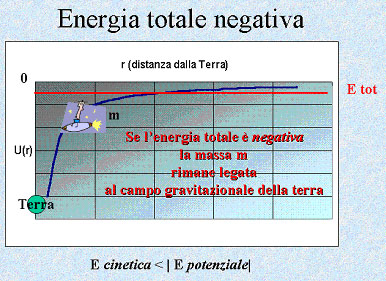
Supponiamo invece che l'energia meccanica E sia negativa. In questo caso si ha che: K < |U|
Nella curva dell'energia in funzione della distanza d dalla Terra, il punto di intersezione dell'energia potenziale U e dell'energia meccanica totale E si dice punto di inversione. Qui l'energia cinetica è nulla e l'energia meccanica totale è solo potenziale.
Quando il meteorite, allontanandosi dalla Terra, raggiunge il punto di inversione, non ha più energia di movimento e non può che essere riattratto dalla Terra, rimanendo quindi intrappolato nel campo gravitazionale terrestre.
Il meteorite intrappolato può cadere sulla Terra oppure rimanere in orbita chiusa attorno ad essa.
Un'orbita chiusa è ellittica ed in essa l'energia si trasforma da potenziale in cinetica e viceversa.
Tornando al problema iniziale, basta calcolare l'energia meccanica E del sistema Terra + meteorite per sapere se esso è in uno stato legato. Il valore della massa m del meteorite non è dato, ma esso può essere messo a fattore comune:
E = m (1/2 v2 - G M / d) = m * 1,87 107 J
La massa m è positiva e quindi l'energia meccanica totale è positiva: il meteorite potrà allontanarsi definitivamente dalla Terra su un'orbita aperta.
| Indice | indietro | avanti |
Copyleft Ludovica Battista