| Indice | indietro | avanti |
Il moto del pendolo
Possiamo considerare armonico il moto del pendolo semplice? La massa m (che può essere schematizzata con un punto materiale) si muove in realtà su un piccolo arco di circonferenza, mentre il moto armonico è un moto rettilineo. Se però ci limitiamo solo a piccole oscillazioni il tratto percorso dal punto materiale può essere considerato quasi rettilineo.
Questo non basta: perché il moto possa dirsi armonico è necessario individuare una forza di richiamo F = - k x proporzionale allo spostamento x della massa dal punto di equilibrio (cioè dalla posizione verticale del pendolo).
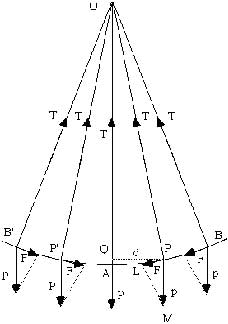
Analizziamo le forze che agiscono sulla massa m: esse sono la forza peso P di modulo m g diretta verticalmente verso il basso e la tensione T diretta nella direzione del filo verso il centro di oscillazione.
Fotografiamo il moto del pendolo in un istante in cui il filo forma un angolo α non nullo (ma piccolo) con la verticale: la forza peso si scompone in una componente radiale diretta come il filo ed una tangenziale diretta nel verso dello spostamento. La tensione del filo è quasi uguale alla componente radiale del peso (la differenza fornirebbe la forza centripeta necessaria per il moto circolare. Però, per piccole oscillazioni (moto praticamente rettilineo), possiamo considerare che tensione e componente radiale del peso si equilibrino e che quindi la forza risultante sul pendolo sia solo la componente tangenziale del peso: F = m g sen α. Questa forza è sempre diretta verso il centro dell'oscillazione, come la forza di richiamo.
Per dimostrare che essa è proporzionale allo spostamento x, ricordiamo che, per piccole oscillazioni, si ha che sen α ~ α, quindi F = m g sen α ~ m g α ~ m g x / L, ricordando che l'angolo α espresso in radianti è dato dal rapporto tra l'arco x e il raggio L.
Esiste quindi un rapporto costante tra l'intensità della forza F e lo spostamento x. La costante elastica k del pendolo è allora: k = F/x = mg/L
| Dati del problema | Richieste | ||
| m = 2 kg | massa del pendolo | T | periodo del pendolo |
| L = 3 m | lunghezza del pendolo |
In un moto armonico semplice il periodo T è legato alla costante elastica k
ed alla massa m dalla relazione
Poiché la costante elastica per un pendolo è a sua volta legata alla massa ed
alla lunghezza L si ottiene:
Il periodo del pendolo semplice è quindi (per piccole oscillazioni) indipendente dalla massa
Dai dati del problema si ottiene: T = 3,47 s
| Indice | indietro | avanti |
Copyleft Ludovica Battista