| Indice | indietro | avanti |
Atomo semiclassico di Bohr
Nel 1913 Niels Bohr propone un modello dell'atomo di idrogeno in grado di spiegare le serie spettroscopiche di questo elemento e degli altri elementi che hanno un solo elettrone nel guscio più esterno. Il modello è detto semiclassico perchè permane la concezione classica dell'elettrone inteso come una particella che ruota intorno al nucleo, corretto da una limitazione quantistica. Sul modello classico di Rutherford, Bohr innesta due condizioni di quantizzazione:
- Per l'elettrone esistono stati permessi (o stazionari) e stati proibiti; sulle orbite stazionarie l'elettrone non irradia energia, in contrasto con le previsioni della fisica classica.
- L'elettrone emette (o assorbe) energia solo se scende (o sale) da un'orbita permessa ad un'altra permessa. La transizione avviene emettendo (o assorbendo) un fotone di frequenza f proporzionale alla differenza di energia ΔE tra i due stati stazionari. La relazione che lega la frequenza del fotone al salto energetico è la relazione quantistica ΔE = h f
Bohr ottenne la condizione per individuare le orbite stazionarie quantizzando il momento angolare dell'elettrone. Un elettrone di massa m che si muove alla velocità v su un'orbita circolare di raggio r possiede un momento angolare di modulo L = m v r che, nella fisica classica, può assumere qualunque valore. Bohr impose che L potesse assumere solo valori discreti tali che:

Bohr propose questa condizione solo perché comoda, senza darne alcuna giustificazione teorica. Undici anni dopo la teoria ondulatoria di De Broglie fornirà al modello atomico di Bohr una convincente ragione teorica, associando all'elettrone una lunghezza d'onda di dimensioni atomiche. Se si abbandona l'idea di una particella classica che ruota su un'orbita per sostituirla con quella di un'onda stazionaria che si chiude perfettamente su tale orbita, si deve avere che sono possibili solo le orbite con circonferenza multipla della lunghezza d'onda associata. Le lunghezze d'onda permesse devono quindi soddisfare la condizione:
n λ = 2 π rn
n h / m v = 2 π rn
m v rn = n h / 2 π condizione di quantizzazione del momento angolare proposta da Bohr
I raggi permessi dell'atomo di idrogeno
Dal punto di vista classico l'elettrone è una particella di massa m e carica e in moto lungo un'orbita circolare di raggio r con velocità di rotazione v. La forza centripeta necessaria alla rotazione è fornita dalla forza di Coulomb. Uguagliando le due espressioni si ottiene:
k e2 / r2 = m v2/r condizione classica
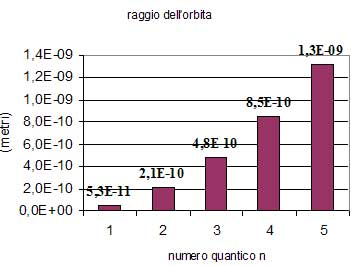
Mettendo a confronto la condizione classica (dove il raggio r può assumere qualsiasi valore) e la condizione di quantizzazione del momento angolare (dove il raggio rn può assumere solo valori discreti) si ottiene (eliminando v):
Il valore del raggio assume valori discreti in funzione del numero quantico principale n. Per n = 1 si ottiene il raggio dell'orbita fondamentale dell'idrogeno. Al crescere del numero quantico n le orbite possibili si allontanano rapidamente dal nucleo e l'attrazione nucleare diminuisce rapidamente.
Livelli energetici del modello di Bohr
Ogni stato stazionario dell'elettrone nell'atomo di idrogeno è caratterizzato da un valore (quantizzato) del raggio e da un valore (sempre quantizzato) dell'energia in funzione del numero quantico principale n. Secondo la fisica classica, l'elettrone in orbita ha energia totale E (cinetica e potenziale) negativa perché l'elettrone di trova in uno stato legato:
l'ultima relazione è stata ottenuta dalla relazione classica v2 = k e2/m r
Poiché sono permessi solo valori discreti del raggio, anche l'energia avrà anch'essa valori discreti. Sostituendo r classico con rn, si ottiene l'energia En in funzione di n.
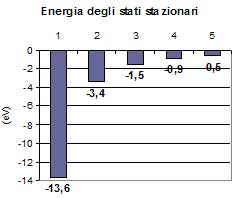
 con E1 = -13.6 eV
con E1 = -13.6 eVPer n = 1 si ha l'energia E1 dello stato fondamentale che coincide (in valore assoluto) con il valore sperimentale dell'energia di ionizzazione dell'idrogeno. Per n > 1 si hanno tutti gli altri possibili livelli energetici (o stati eccitati) per l'elettrone dell'atomo di idrogeno.
Per raggiungere lo zero ci sono infiniti livelli, ma la loro distanza "energetica" diventa sempre minore. All'aumentare del numero quantico, i livelli energetici salgono con una serie infinita di gradini verso il livello zero e il lavoro richiesto per spostare l'elettrone da un orbita all'altra è sempre più piccolo. Lo stato di elettrone libero corrispondente ad una energia nulla è un limite per n che tende a infinito.
La teoria di Bohr afferma che i livelli En sono stazionari, (secondo la teoria quantistica i livelli stazionari corrispondono a determinate onde stazionarie). Un elettrone può saltare da un livello ad uno superiore se riceve da un fotone l'energia necessaria al salto, cioè se assorbe energia. Un elettrone che occupa uno stato diverso dallo stato fondamentale di dice eccitato. Lo stato di eccitazione non è stabile e l'elettrone decade rapidamente verso i livelli inferiori emettendo energia sotto forma di un fotone.
Se il livello energetico finale è maggiore di quello iniziale significa che il fotone viene assorbito dall'atomo (eccitazione), se invece il livello finale è minore di quello iniziale, il fotone viene emesso dall'atomo durante la transizione (diseccitazione).
L'atomo di Bohr su Physics 2000Alla luce di queste considerazioni, la formula empirica di Balmer si interpreta attribuendo ad ogni possibile salto dell'elettrone una diversa riga dello spettro dell'idrogeno. Per ogni transizione si ha:

La teoria di Bohr spiega la ragione degli spettri a righe degli atomi: Ogni riga colorata di uno spettro di emissione corrisponde all'emissione di un fotone durante una diseccitazione, le righe scure dello spettro di assorbimento rappresentano invece i fotoni assorbiti durante una eccitazione. I numeri che nella formula di Balmer individuano la serie e la riga rappresentano quindi i numeri quantici principali dei due livelli interessati al salto. Per quanto riguarda lo spettro di emissione, tutti i salti quantici che finiscono sul livello fondamentale n = 1 formano la serie di Lymann (nell'ultravioletto, quindi con maggiore energia), quelli che finiscono sul livello n = 2 formano la serie di Balmer (visibile), quelli che finiscono sul livello n = 3 formano la serie di Paschen (infrarosso). Le altre serie coinvolgono energie sempre minori perché corrispondono a salti quantici sempre minori. L'intensità delle righe dipende invece dal numero di transizioni da parte di più atomi.
| Indice | indietro | avanti |
Copyleft Ludovica Battista