| Indice | indietro | avanti |
Intervallo invariante
A volte capita di sentir riassumere la teoria della relatività con l'espressione tutto è relativo. L'espressione è superficiale e profondamente sbagliata. Basterebbe rileggere il principio di relatività di Galileo che rimane invariato nella relatività di Einstein: Le leggi della fisica sono le stesse in tutti i riferimenti inerziali. Come spesso succede, siamo interessati a ciò che rimane costante più che a ciò che varia. L'attenzione è rivolta alle grandezze invarianti. Fra queste c'è naturalmente la velocità della luce nel vuoto che ha lo stesso valore in tutte le direzioni e in tutti i sistemi di riferimento inerziali.
Il problema è che le grandezze invarianti non sono quelle che il senso comune farebbe supporre. In definitiva, su cosa concordano gli osservatori di due sistemi di riferimento inerziali? Riprendiamo l'esempio dell'orologio a luce e consideriamo la separazione spaziale e la separazione temporale tra i due eventi PARTENZA e ARRIVO del raggio di luce.
 |
 |
Nel riferimento solidale all'orologio si ha che i due eventi hanno: Separazione temporale T0 = 2 d /c Separazione spaziale nulla T0 è l'intervallo di tempo proprio |
Nel riferimento in cui l'orologio è in moto con velocità v i due eventi hanno: Separazione temporale T = 2 L /c Separazione spaziale è s = 2 x (tratto percorso dall'orologio nel tempo T) T non è un tempo proprio (il tempo proprio è quello misurato tra due eventi con separazione spaziale nulla) |
Se l'orologio a luce fosse posto su un treno con velocità v' diversa da v le misure di tempo e spazio cambierebbero ancora da un riferimento all'altro. Quale, tra le seguenti misure di spazio e tempo, è invariante nei diversi sistemi di riferimento inerziali in moto uniforme l'uno rispetto all'altro?
la separazione temporale tra i due eventi
la separazione spaziale tra i due eventi
lo spazio percorso dalla luce
la distanza tra i due specchi dell'orologio
La distanza tra i due specchi dell'orologio non subisce variazioni in quanto è perpendicolare alla direzione del moto: essa è una quantità invariante. Vediamo di esprimerla in funzione delle altre grandezze che dipendono dal riferimento. Con una semplice relazione pitagorica si ha:
| Riferimento | Distanza percorsa dalla luce | Distanza percorsa dall'orologio (separazione spaziale) |
| Solidale all'orologio | 2 d | 0 |
| In moto relativo a velocità v | 2 L | s = 2 x |
| In moto relativo a velocità v' | 2 L' | s' = 2 x' |
La relazione che esprime d può essere scritta:
 e, moltiplicando tutto per 2, abbiamo:
e, moltiplicando tutto per 2, abbiamo:
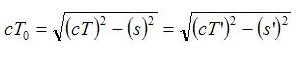
Questa grandezza si chiama intervallo invariante. Esso tiene conto sia della separazione spaziale, sia della separazione temporale tra due eventi. Si ottiene facendo la radice della differenza tra due quadrati: la distanza percorsa dalla luce nella separazione temporale e la separazione spaziale.
| Indice | indietro | avanti |
Copyleft Ludovica Battista