| Indice | indietro | avanti |
Legge di Biot Savart
Un conduttore rettilineo è percorso da una corrente i = 1,3 mA. Immagina due percorsi chiusi intorno al filo: uno circolare di raggio 3 cm ed uno quadrato di lato 3 cm. Cosa si può dire della circuitazione di campo magnetico lungo questi due percorsi?
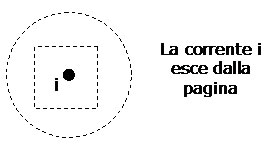
La circuitazione è maggiore nel percorso circolare
La circuitazione è maggiore nel percorso quadrato
La circuitazione è la stessa nei due percorsi
La legge di Ampère 
dice che la circuitazione dipende solo dalle correnti concatenate al percorso: in questo caso l'unica
corrente concatenata è i e la circuitazione in ambedue i casi vale:
C(B) = μ0 i = 1,64 10-9 T m2
Il fatto che la circuitazione dipenda dalle correnti concatenate significa che il campo magnetico non è conservativo, ma ci permette di avere anche altre informazioni sul campo magnetico creato dalle correnti. Analizziamo meglio il semplice caso di un singolo conduttore rettilineo percorso da corrente: come varia il campo magnetico nello spazio circostante?
| Dati del problema | Richieste | ||
| i = 1,3 mA | corrente nel conduttore | B (r) | valore del campo B alla distanza r |
| r = 3 cm | distanza dal conduttore |
Come abbiamo detto, la circuitazione del campo B vale: C(B) = μ0 i. Affrontiamo ora la somma integrale: scegliamo il percorso circolare di raggio r con verso di percorrenza antiorario. Questa scelta è conveniente perché il campo magnetico ha linee di forza circolari ed è quindi in ogni punto parallelo all'elemento infinitesimo dl. Inoltre, per ragioni di simmetria l'intensità del campo sarà costante in tutti punti della circonferenza.
Il prodotto scalare di due vettori paralleli è semplicemente il prodotto B dl dei moduli (il coseno dell'angolo compreso è 1) ed il fattore B può essere messo a fattor comune (l'integrale si comporta come una somma). A questo punto l'integrale è immediatamente risolvibile: esso rappresenta una somma di spostamenti dl infinitesimi estesa a tutto il percorso circolare, quindi il suo valore è la lunghezza della circonferenza di raggio r, cioè 2 π r. Mettendo insieme il valore della circuitazione trovata con la legge di Ampère e quella trovata con l'integrale si ottiene:
μ0 i = B 2 π red è quindi possibile ricavare il valore del campo magnetico B ad una distanza r dal filo:
Il campo magnetico creato da un conduttore rettilineo percorso da corrente ha un'intensità proporzionale alla corrente e inversamente proporzionale alla distanza dal filo.
Per quanto riguarda il problema in esame, il campo B a 3 cm dal filo percorso da una corrente di 1,3 mA vale: B = 8,69 nT
Per visualizzare il verso delle linee di campo si usa la nota regola della mano destra: il pollice va nel verso della corrente e le altre dita si avvolgono intorno al filo secondo il verso delle linee di campo.
Allo stesso risultato giunsero, sperimentalmente, i fisici Jean Baptiste Biot (1774 - 1862) e F. Savart (1791-1841) sempre nel 1820. Per questa ragione la legge è anche chiamata legge di Biot- Savart. Naturalmente il campo magnetico prodotto dal filo non esercita alcuna forza sul filo stesso, così come una carica elettrica non subisce forze da parte del proprio campo elettrico.
| Indice | indietro | avanti |
Copyleft Ludovica Battista