| Indice | indietro | avanti |
Simmetria sferica: campo radiale
Una carica puntiforme Q genera un campo a simmetria radiale: tutte le linee di campo escono (o entrano) nel punto in cui si trova la carica sorgente. La direzione del campo è centrifuga se la carica Q è positiva, centripeta se è negativa. La densità delle linee diminuisce man mano che ci si allontana dalla sorgente: il campo quindi non è uniforme, ma la sua intensità in un punto dipende dipende dalla distanza del punto dalla sorgente.
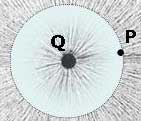
Per determinare l'intensità di E(P) in un punto P si utilizza ancora una volta la legge di Gauss, scegliendo una superficie gaussiana di opportuna simmetria che contenga la carica sorgente Q. La scelta ovvia è una superficie sferica centrata su Q con raggio uguale alla distanza d del punto P dalla carica Q.
Il flusso attraverso la superficie sferica è, per la legge di Gauss: Φ (E) = Q / ε0
Il flusso si calcola, per definizione, con la somma integrale:
![]()
La simmetria della superficie sferica evita di dover ricorrere al calcolo integrale, infatti
i vettori E e dA sono sempre paralleli e concordi, quindi il
loro prodotto scalare vale E dA. Inoltre l'intensità E del campo è la stessa per qualunque punto
a distanza d dalla carica centrale. Poiché l'integrale non è altro che una somma, E può essere messo
a fattor comune: ![]()
L'integrale rappresenta ora la sommatoria di tutte le superfici infinitesime dA estesa a tutta la superficie sferica e quindi ha come risultato la superficie della sfera:
Φ (E) = E 4 π d2Uguagliando le due espressioni ottenute per il flusso si ottiene l'intensità del campo E.
Il campo elettrico in un punto P di un campo radiale distante d dalla carica puntiforme Q è inversamente proporzionale al quadrato della distanza d.
E(P) = k Q / d2con k = 1 / 4 π ε0 = 9 109 Nm2/C2
L'intensità E del campo è determinata dal valore assoluto |Q| della carica. Con una carica negativa, l'intensità E è la stessa, ma cambia il verso del vettore e quindi delle linee di campo.
Legge di Coulomb
La legge di Coulomb può essere facilmente dedotta dalla legge precedente e quindi dalla legge di Gauss: se una seconda carica q si trova nel punto P (a distanza d dalla carica sorgente Q) essa risentirà di una forza elettrica di intensità:
F = q E(P) = k Q q / d2con k = 1 / 4 π ε0
Naturalmente possiamo dire sia che q si trova nel campo creato da Q, sia che Q si trova nel campo creato da q.
| Indice | indietro | avanti |
Copyleft Ludovica Battista