| Indice | indietro | avanti |
Energia interna
L'energia interna U di un gas è data dalla somma di tutte le energie cinetiche delle particelle (in un gas perfetto si assume che l'energia potenziale sia nulla) e inoltre, se le molecole sono rappresentabili come punti materiali, l'energia cinetica è solo energia di traslazione.
La traslazione è un moto d'insieme in cui tutte la parti di un corpo compiono lo stesso spostamento nello spazio tridimensionale e può essere scomposta in 3 direzioni spaziali indipendenti. Si dice che la traslazione ha 3 gradi di libertà
Se si considerano molecole più complesse dotate di una loro struttura interna, si deve conseguentemente tener conto di altri tipi di energia cinetica legati ad altri moti come la rotazione o la vibrazione. Una molecola più complessa ha quindi più gradi di libertà.
L'energia cinetica media di traslazione è, per definizione, la media aritmetica di tutte le energie cinetiche delle particelle microscopiche. Con N particelle di massa m, dotate di velocità v1 .. vN, l'energia cinetica media di traslazione è:
Sostituendo alla velocità quadratica media l'espressione
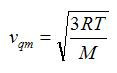, si ottiene:
dove k è la costante di Boltzmann.
| Dati del problema | Richieste | ||
| n = 1 mol | numero di moli | K | energia cinetica media di traslazione |
| T = 300 K | temperatura del gas | U | energia interna del gas |
| Gas monoatomico |
L'energia cinetica media di traslazione si calcola direttamente con la relazione appena vista
= 6,21 10-21 J
L'energia interna U di un gas ideale monoatomico è data dalla somma di tutta l'energia cinetica di traslazione e si ottiene quindi moltiplicando l'energia cinetica media per il numero N di particelle.
U = 3/2 N k T = 3/2 N R / NA T = 3/2 n R T = = 3739,5 J
L'energia interna U di un gas ideale dipende solo dalla temperatura e dal numero delle moli. Una mole di un qualunque gas perfetto monoatomico a 300 K ha un'energia interna di 3739,5 J
Mettiamo a confronto le due espressioni trovate per l'energia, a livello microscopico e macroscopico:
|
Energia cinetica media di una molecola (grandezza microscopica) |
 |
Energia interna di n moli di un gas monoatomico (grandezza macroscopica) |
Si noti:
- il ruolo delle due costanti k e R: la costante di Boltzmann è legata alle singole molecole mentre la costante R riguarda tutto il gas.
- il fattore 3/2 dipende dai tre gradi di libertà possibili della traslazione (movimento lungo 3 direzioni spaziali).
In un diagramma pressione-volume un ramo di iperbole caratterizza una particolare isoterma ed è associato ad un determinato valore della temperatura e dell'energia interna.
| Dati del problema | Richieste | ||
| T1 = 300 K | temperatura dell'isotema più bassa | U (T1) | energia interna alla temperatura T1 |
| T2 = 500 K | temperatura dell'isotema intermedia | U (T2) | energia interna alla temperatura T2 |
| T3 = 1000 K | temperatura dell'isotema più alta | U (T3) | energia interna alla temperatura T3 |
| n = 1 mol | numero di moli | ΔU | variazione di energia interna in una qualunque trasformazione da T1 a T3 |
| Gas monoatomico |
Il calcolo delle 3 energie è immediato:
U(T1) = 3/2 mol 8,31 J K-1mol-1 300 K = 3739,5 J
U(T2) = 3/2 mol 8,31 J K-1mol-1 500 K = 6232,5 J
U(T3) = 3/2 mol 8,31 J K-1mol-1 1000 K = 12 465,0 J
e quindi ΔU = U(T3) - U(T1) = 8725,5 J
Dal momento che l'energia interna è la stessa per ogni punto dell'iperbole, la variazione di energia interna del gas per andare da uno stato a temperatura 300 K ad un altro stato a temperatura 1000 K sarà sempre la stessa, indipendentemente dal tipo di trasformazione seguita.
L'energia interna varia solo se in una trasformazione c'è una variazione di temperatura. Possiamo scrivere:
| Indice | indietro | avanti |
Copyleft Ludovica Battista