| Indice | indietro | avanti |
Potenza elettrica
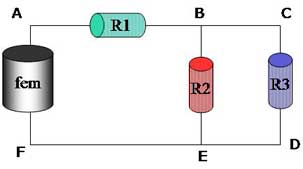
| Dati del problema | Richieste | ||
| ε = 100 V | fem del generatore | P | potenza fornita |
| i = 45,5 mA | corrente principale |
Ricordiamo tre definizioni:
- La potenza è l'energia fornita nell'unità di tempo.
- La forza elettromotrice è definita come lavoro fatto sull'unità di carica.
- La corrente è la carica che attraversa una sezione del circuito nell'unità di tempo.
Mettendo insieme le tre osservazioni, si ha che
Potenza = Lavoro / tempo = ε carica / tempo = ε i
Con i nostri dati, la potenza del generatore vale P = 100 V * 45,5 mA = 4,55 W
La potenza fornita viene dissipata nelle resistenze del circuito che si riscaldano (effetto Joule).
Per ogni resistenza vale un'analoga relazione:
Potenza dissipata da R1 = VAB i
Potenza dissipata da R2 = VBE i2
Potenza dissipata da R1 = VBE i3
dove i, i2 e i3 sono le correnti che attraversano ogni resitenza e VAB, VBE sono le differenze di potenziale ai capi di R1 e del parallelo. Applicando la legge di Ohm alle tre resistenze si ottiene:
Potenza dissipata da R1 = R1 i2
Potenza dissipata da R2 = R2 i22
Potenza dissipata da R1 = R3 i32
| Dati del problema | Richieste | ||
| ε = 100 V | fem del generatore | P1 | potenza dissipata in R1 |
| i = 45,5 mA | corrente che attraversa R1 | P2 | potenza dissipata in R2 |
| R2 = 2000 Ω | resistenza R2 | P3 | potenza dissipata in R3 |
| R3 = 2000 Ω | resistenza R3 |
Per determinare il valore della resistenza R1, possiamo determinare la resistenza equivalente del circuito e sottrarre il valore del parallelo:
Requivalente = ε / i = 100 V / 45,5 mA = 2200 Ω
Il parallelo di R2 e R3 (formato da due resistenze uguali) vale RP = 1000 Ω
Quindi R1 = 1200 Ω
Le correnti i2 e i3 sono uguali, perchè sono uguali le resistenze nei due rami del parallelo. Ne consegue che la corrente principale i si divide in due parti uguali:
i2 = i3 = 22,75 mA
e quindiP1 = R1 i2 = 2,48 W
P2 = R2 i22 = 1,035 W
P3 = R3 i32= 1,035 W
Nei limiti delle approssimazioni di calcolo, si ha che la potenza fornita dal generatore è uguale alla potenza dissipata totale.
| Indice | indietro | avanti |
Copyleft Ludovica Battista