| Indice | indietro | avanti |
Legge del nodo
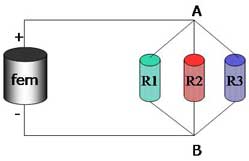
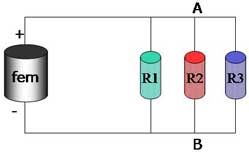
Consideriamo il circuito in figura (le due figure sono equivalenti) formato da un generatore ideale di forza elettromotrice ε e tre resistenze di valore R1, R2 e R3 collegate in parallelo.
Sia ΔV la differenza di potenziale tra il punto A e il punto B. Nel circuito sono presenti due nodi in cui la corrente principale si divide nei tre rami contenenti rispettivamente le resistenze R1, R2 e R3.
| Dati del problema | Richieste | ||
| ε = 100 V | fem del generatore | i | corrente principale nel ramo del generatore |
| R1 = 1200 Ω | resistenza R1 | i1 | corrente nel ramo di R1 |
| R2 = 2000 Ω | resistenza R2 | i2 | corrente nel ramo di R2 |
| R3 = 500 Ω | resistenza R3 | i3 | corrente nel ramo di R3 |
Nel problema ci sono 4 incognite, quindi occorrono 4 relazioni indipendenti. Come sappiamo, nella risoluzione dei circuiti si utilizzano le due leggi di Kirchhoff: la legge del nodo e la legge della maglia. Se la legge della maglia è una legge di conservazione dell'energia, quella del nodo è un modo di esprimere la legge di conservazione della carica elettrica. La legge del nodo dice in sostanza che la carica non si crea nè si distrugge e quindi che la corrente che entra in un nodo deve essere uguale alla corrente che ne esce.
Convenzione dei segni per le correnti: una corrente è positiva se esce dal nodo, negativa se entra nel nodo.
- i positiva, i1, i2, i3 negative
- i negativa, i1, i2, i3 positive
Per la legge del nodo si ha: - i + i1 + i2 + i3 = 0 cioè i = i1 + i2 + i3.
Applichiamo la legge della maglia alla maglia che contiene il generatore e una delle resistenze, per esempio la resistenza R1, percorrendo il circuito in senso orario:
ε - ΔV = 0
Poichè le resistenze sono in parallelo, la caduta di potenziale è la stessa ai capi di tutte e tre le resistenze:
ΔV = i1 R1 = i2 R2 = i3 R3
Dalla relazione ε - i1 R1 = 0 si ottiene i1 = ε / R1
Dalla relazione ε - i2 R2 = 0 si ottiene i2 = ε / R2
Dalla relazione ε - i3 R3 = 0 si ottiene i3 = ε / R3
Naturalmente la corrente che circola in ogni ramo è inversamente proporzionale alla resistenza del ramo. Sostituendo i dati in tabella si ha:
| i1 = 0,08 A | i2 = 0,05 A | i3 = 0,20 A | i = 0,33 A |
Mettendo insieme le quattro relazioni sulle correnti, si ha:
i = i1 + 12 + 13 = ε/R1 + ε/R2 + ε/R2 = ε (1/R1 + 1/R2 + 1/R3)
i = ε / Req
1 / Req = 1/R1 + 1/R2 + 1/R3 + ...
La resistenza equivalente del parallelo del circuito in esame è:
| Req = 300 Ω |
La resistenza equivalente ad un parallelo è minore di ogni resistenza del parallelo!
| Indice | indietro | avanti |
Copyleft Ludovica Battista