| Indice | indietro | avanti |
Legge di Gauss per il magnetismo
Come per il campo elettrico, anche per il campo magnetico esiste una legge analoga a quella formulata dal grande matematico tedesco K. F. Gauss (1777-1855). Ricordiamo che la legge di Gauss (una delle leggi di Maxwell dell'elettromagnetismo) descrive una caratteristica importante del campo elettrostatico: l'esistenza di punti singolari dove sono poste le cariche sorgenti del campo e dove le linee di campo nascono o muoiono. Rivediamo questa legge:
Legge di Gauss per il campo elettrico E

Il flusso elettrico attraverso una superficie gaussiana è direttamente proporzionale alla somma algebrica di tutte le cariche elettriche presenti all'interno della superficie.
La costante ε0 è la costante dielettrica del vuoto ε0 = 8,85 10-12 C2 / N m2
La legge di Gauss per il magnetismo (un'altra delle leggi di Maxwell) afferma una cosa diversa:
Legge di Gauss per il campo magnetico B
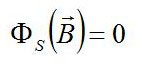
Il flusso magnetico attraverso una superficie gaussiana è sempre nullo.
Il campo magnetico non ha sorgenti
Le linee di campo magnetico sono sempre linee chiuse
Il campo magnetico non è conservativo
Non esistono monopoli magnetici

Le linee di campo di un dipolo magnetico sono diverse da quelle di un dipolo elettrico formato da due cariche opposte.
Se il flusso del campo magnetico è sempre nullo, significa che non esistono nel campo dei punti singolari dove le linee nascono o muoiono, altrimenti potrebbe essere costruita una superficie gaussiana intorno a questo punto ed avere un flusso positivo o negativo: il campo magnetico non ha sorgenti.
Per la stessa ragione, se le linee non nascono e non muoiono, esse devono essere sempre linee chiuse, senza inizio né fine. Il campo magnetico terrestre, per esempio, ha delle linee che fuori della Terra vanno dal nord al sud magnetico, ma dentro la Terra vanno dal sud al nord magnetico senza soluzione di continuità.
L'unica affermazione che non è conseguenza della legge di Gauss per il magnetismo è: il campo magnetico non è conservativo. Questo è vero (ed è un'altra importante differenza con il campo elettrostatico), ma il fatto che un campo sia o meno conservativo non dipende dal flusso del campo, ma dalla circuitazione: Un campo è conservativo se la circuitazione è sempre nulla.
| Indice | indietro | avanti |