| Indice | indietro | avanti |
Modello di Ehrenfest
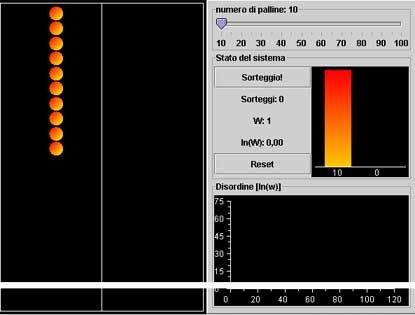
Il modello da considerare, che puoi sperimentare nelle Simulazioni del sito, è un sistema formato da un contenitore diviso in due sezioni A e B e da un certo numero di palline numerate.
Nello stato iniziale tutte le palline sono nella prima sezione e la seconda è vuota.
In base ad un sorteggio casuale (per esempio un sacchetto contenente i numeri corrispondenti alle palline) si determina il passaggio di una pallina da una sezione all'altra.
Dopo, il numero viene reintrodotto nel sacchetto e si procede ad una nuova estrazione: ogni volta la pallina corrispondente al numero estratto passa da una sezione all'altra.
Come evolverà il sistema?
Lo stato iniziale del sistema (o macrostato) è: (10 palline in A; 0 in B)
Dopo la prima estrazione, si ha la trasformazione dal macrostato (10; 0) al macrostato (9; 1)
Qualsiasi numero tra 1 e 10 sia stato estratto, si avrà sempre lo stesso macrostato. Nel macrostato non si fa differenza tra una pallina e l'altra.
Se chiamiamo microstato, una situazione in cui riconosciamo la posizione di ogni pallina si avrà che
Il valore W associato ad un macrostato è detto grado di disordine del macrostato
- Dal macrostato (9; 1) al macrostato (10; 0)
- Dal macrostato (9; 1) al macrostato (8; 2)
Al macrostato (8;2) corrisponde un grado di disordine W molto più elevato, corrispondente al numero di modi in cui si possono raggruppare 2 elementi in un insieme di 10.
Il calcolo combinatorio permette di calcolare il numero W dei microstati possibili per un generico macrostato (NA; NB)
con N = NA + NB
| Macrostato | Grado di disordine W | Macrostato | Grado di disordine W |
| (10; 0) | 1 | (9; 1) | 10 |
| (8; 2) | 45 | (7; 3) | 120 |
| (6; 4) | 210 | (5; 5) | 252 |
Il sistema evolve verso stati più probabili, cioè verso quelli con un grado di disordine più alto: niente vieta di tornare verso stati più ordinati, ed infatti tali fluttuazioni avvengono, ma la tendenza generale è quella di andare verso lo stato di massimo disordine, cioè lo stato (5; 5) che sembra abbastanza stabile: una volta raggiunto è difficile (cioè improbabile, ma non impossibile) allontanarsene.
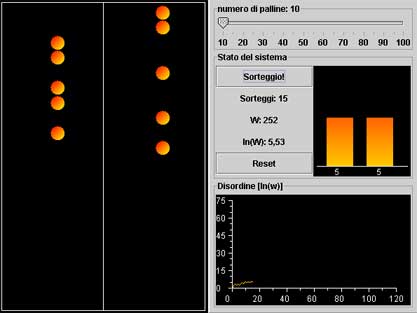
Lo stato più disordinato corrisponde alla massima incertezza sulla posizione di una singola pallina: il concetto di disordine è collegato a quello di mancanza di informazioni.
Un sistema con meno palline ha maggiori probabilità di riordinarsi. Per rendersene conto, basta eseguire la simulazione variando il numero delle palline.
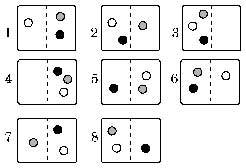
In un gas, il numero di particelle componenti è enorme (dell'ordine del numero di Avogadro!) e ogni macrostato termodinamico, caratterizzato da valori stabili delle grandezze di stato, corrisponde ad un enorme grado di disordine: ne consegue che la probabilità di andare spontaneamente verso stati più ordinati, come quello in cui tutte le molecole occupino per caso la metà del volume a disposizione, è praticamente trascurabile!
Come si è potuto intuire, la grandezza microscopica legata all'entropia è proprio il grado di disordine del sistema.
L'asserzione secondo cui un sistema evolve spontaneamente verso stati di entropia maggiore puo' tradursi in:
Ludwig Boltzmann ha trovato la seguente relazione tra l'entropia S in un determinato stato ed il grado di disordine W corrispondente:
con k = 1,38 10-23 J/K costante di Boltzman
| Indice | indietro | avanti |